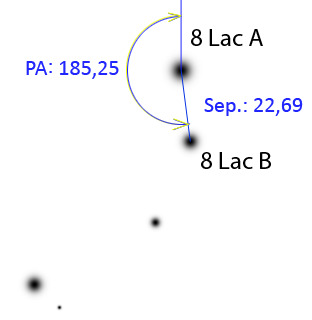
Calc of the angular separation between 2 sets of coordinates and relative position angle
First coordinates AR / Decl		Quick entry of coordinates in (AR Decl): hh mm ss gg mm ss
Seconds coordinates AR / Decl		Quick entry of coordinates in (AR Decl): hh mm ss gg mm ss

(Right Ascension)					(Declination)
	Hours	Minutes	Seconds			Degree	Minutes	Seconds
α1					δ1
α2					δ2

A.R.1 in g.ddd		A.R.1 in h.ddd				Decl.1 in g.ddd
A.R.2 in g.ddd		A.R.2 in h.ddd				Decl.2 in g.ddd

Delta A.R. in degrees e decimals:
Delta Decl. in degrees e decimals:

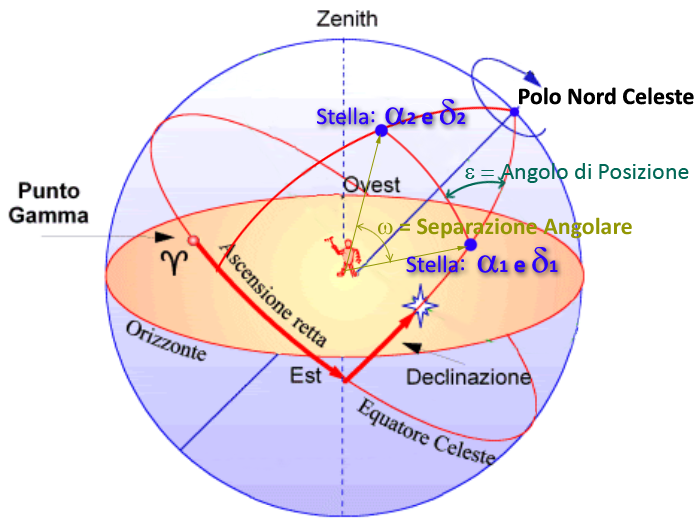
ω Angular Separation (radian):	ω Angular Separation (Sexagesimal):		ε Position Angle (Sexagesimal):

La Separazione Angolare ω tra 2 stelle di coordinate (α1; δ1) e (α2; δ2) è data dalla formula:
cos(ω) = sin(δ1) sin(δ2) + cos(δ1) cos(δ2) cos(α2 - α1)

L'Angolo di Posizione ε è l'angolo (del triangolo sferico) compreso tra il cerchio massimo passante per la coppia di coordinate delle 2 stelle e il meridiano passante per le coordinate della prima stella, misurato in senso antiorario (da nord a est) ruotando intorno alle coordinate AR e Decl della prima stella.

Per calcolare tale angolo, ho usato la seguente espressione trigonometrica:
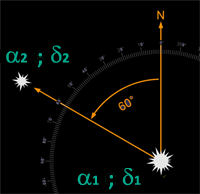
tan(ε) = ( cos(δ1) cos(δ2) sin(α2 - α1) ) / (sin(δ2) - cos(ω) sin(δ1) )

Si definisce triangolo sferico la superficie sulla sfera limitata da tre archi passanti per i cerchi massimi e per tre punti detti vertici.